「自分の飛距離の〈平均値〉を把握せよ」っていうフレーズにひっかっかる。いわんとするところは理解できて,〈最大値〉なくて〈平均値〉,つまり〈現実〉を見ろってことだけど,その〈平均値〉っていうのがね,統計学を齧った人間からすると違和感いだくわけですよ。
統計の世界でよくきく,こんなジョークがあります。
統計学者が,頭をオーブンに突っ込んで,両足を氷水につけている。いまどんな気分かと訊かれたその統計学者は,「うん,平均的にはいい気分だね」*1
ジョークといいつつ笑えないんですが,要するに「平均をとることで,その裏にあるデータの多様性が失われる」ということかと*2。
具体例をあげましょう。たとえばドライバーショットのキャリーが〈5割の確率で300yd,残り5割の確率で200yd〉という人がいたとする。この人の平均キャリーはもちろん〈250yd〉だけど,この数字にどれだけの意味があるのか,っていう。
東京クラシックの13番パー4。いかにもニクラウス設計ぽい明白な〈リスク・リワード〉ホール。

ここで上の例の人が「俺のティーショットは平均250ydキャリーだから,池越え狙うぞ!」ってなります? ならないでしょ。5割の確率で池なんだから――そういうギャンブルを好む人が少なからずいるのは分かりますが。
もちろんこれは極端な例で,現実的にはもっと連続的に分散してるでしょう。こんな感じで。
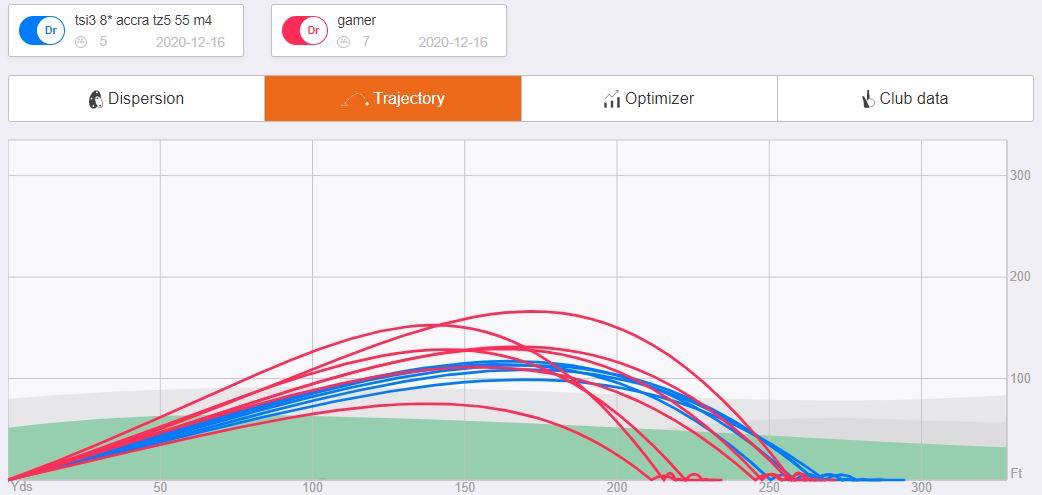
このときに把握すべきは,
- いちばん起こりうる結果はどれか(最頻値)
- 起こりうる結果の幅の真ん中はどれか(中央値)
- 〇〇yd以上だったら△△パーセントの確率で打てる(パーセンタイル)
だと思うんですよね。上記の池越えのケースならば〈パーセンタイル〉が重要になってくる。つまり仮に245ydで池をキャリーできるとして,その245ydが自分にとって10パーセンタイルなのか(10回に1回は失敗する)25パーセンタイルなのか(4回に1回は失敗する)50パーセンタイルなのか(2回に1回は失敗する)を把握する,ってことですよね。あとはご自身の好みで選択してくださいって感じで。
そういえば,しぶこが全英オープン勝ったときのバックナインでの池越えのドライバーショット。あれ本人はどれぐらいの成功確率だと思って打ったのかなあ。
余談
「ナイスショットしたからミスした」(ドッグレッグで突き抜けたとか,グリーンをオーバーしたとか)って言う人いるけど,そもそもナイスショットがミスになるような選択(ライン取りでもクラブ選択でも)してる時点でおかしいでしょ。ナイスショットすることを恐れて球打ってたら上達は望めないと思います。
さらに余談
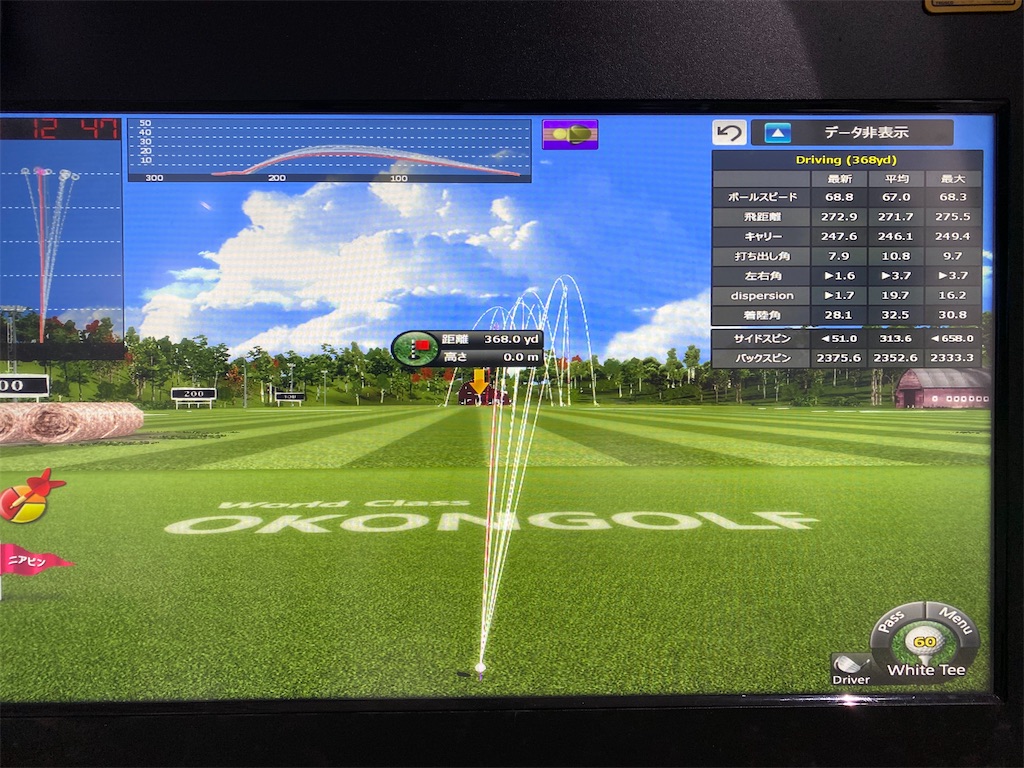
ためしに10球打ってみたら,こんな感じでした。縦より横の散らばりが大きいです。